（本貼文所列出的程式碼，皆以 colab 筆記本方式執行，[可由此下載]
(https://colab.research.google.com/drive/1g5BmTsItir8neTA59wvYzvrDqbbM_4aK?usp=sharing)

藉由多個 jax.grad() 呼叫組合，我們可以輕易的求取高階導函數的值。我們先從一元函式說起，接著再來探討 Auto Diff 如何處理多元函式的高階導函數 [27.1]。

一元函式

考慮下列函式以及它的前四階導函式（用手算出來）：

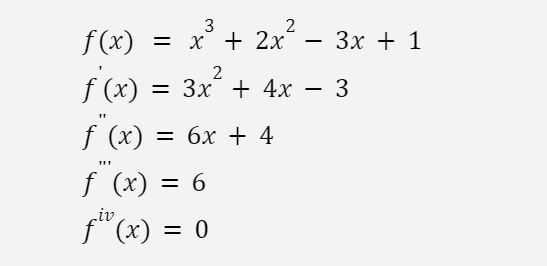
當 x = 1 ，它的各階導函數分別是：

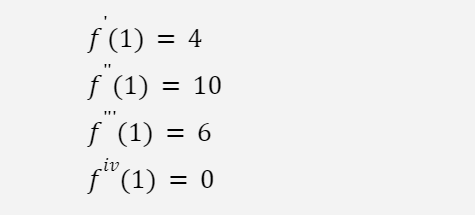
組合數個 jax.grad 可以很方便的求取這些導函數：

f = lambda x : x**3 + 2*x**2 - 3*x + 1
 
# 1st order
print(f'1st order : {grad(f)(1.)}')
# 2nd order
print(f'2nd order : {grad(grad(f))(1.)}')
# 3rd order
print(f'3rd order : {grad(grad(grad(f)))(1.)}')
# 4th order
print(f'4th order : {grad(grad(grad(grad(f))))(1.)}')

output:
1st order : 4.0
2nd order : 10.0
3rd order : 6.0
4th order : 0.0

多元函式的二階導數

多元函式的高階導函式比較複雜，我們先來看看第二階的例子。在數學上一般使用「海森矩陣 Hessian matrix」[27.2] 來表示二階導數。

黑塞矩陣（德語：Hesse-Matrix；英語：Hessian matrix 或 Hessian），又譯作海森矩陣、海塞（賽）矩陣或海瑟矩陣等，是一個由多變量實值函數的所有二階偏導數組成的方塊矩陣，由德國數學家奧托·黑塞引入並以其命名。
…

…
函數 f 的黑塞矩陣和雅可比矩陣有如下關係：函數 f 的黑塞矩陣等於其梯度的雅可比矩陣。

JAX 除了提供直接計算海森矩陣的方法，也有計算梯度 (就是計算導函數的 grad ) 和計算雅可比矩陣的 API，我們可以組合這兩個 API 達到相同的目的。

此外，JAX 提供了兩種計算雅可比矩陣的方法，順向雅可比計算 (jacfwd) 和逆向雅可比計算 (jacrev) 。這兩個 API 計算結果一樣，它們的差異性在於：

• 不同的函式 f ，這兩個 API 的執行效率 (速度) 不同，某些類型的函式，順向比較快；而某些類型則逆向比較快。
• 函式內如果有 while_loop，或 fori_loop，則不要使用逆向。

下面的例子，說明了以上的這三種方法：

def hessian_fwd(f):
    return jacfwd(grad(f))
 
def hessian_rev(f):
    return jacrev(grad(f))

def f(X):
    return jnp.dot(X,X)
 
X = jax.numpy.array([1.,2.,3.])
 
print(f'Hessian')
print(hessian(f)(X))
print(f'FWD mode:')
print(hessian_fwd(f)(X))
print(f'REV mode:')
print(hessian_rev(f)(X))

output:
Hessian
[[2. 0. 0.]
[0. 2. 0.]
[0. 0. 2.]]
FWD mode:
[[2. 0. 0.]
[0. 2. 0.]
[0. 0. 2.]]
REV mode:
[[2. 0. 0.]
[0. 2. 0.]
[0. 0. 2.]]

有關 Auto Diff 老頭就先介紹到這裏，未來有機會，針對某些特定的應用，再陸續的說明其他進階的功能，請大家拭目以待。

註：

[27.1] 本文主要是參考 JAX 官網文件 「Higher-order derivatives」

[27.2] 海森矩陣，可參考維基百科「黑塞矩陣」